CALCULO ALExTREMO - limites laterales

LIMITES LATERALES

Para probar que una funcion tenga limite es necesario probar que tanto por la derecha, como por la izquierda se aproximan a un mismo numero

El límite lateral por la izquierda de una función y=f(x) en el punto x = a es el valor al que se aproxima f(x) cuando x se aproxima al valor de a por valores menores que a . Lo representamos por :

EJEMPLO:

Por izquierda

**Figura: $lim_{x=3-}=5$**

El límte lateral por la derecha de una función y = f(x) en el punto x = a es el valor al que se aproxima f(x) cuando x se aproxima al valor de a por valores mayores que a . Lo representamos por :

Por derecha ver la (fig 2)

**Figura 2: $lim_{x=3}=5$**

EL LIMITE DE LAS DOS GRAFICAS ES:

$begin{displaymath}lim_{x=3}=5 end{displaymath}$

Ejemplo :

El límite de una función en un punto si existe, es único.

En este caso vemos que el límite tanto por la izquierda como por la derecha cuando x tiende a 2 es 4.

El límite de la función es 4 aunque la función no tenga imagen en x = 2.

Ejemplo

f(x) =  x² si x <= 2
        -2x + 1 si x > 2

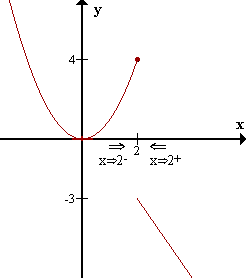lim_x->2-f(x)=4
lim_x->2+f(x)=-3
No existe lim_x->2f(x)